Los activistas de la Corte Suprema que se oponen a la tutela partidista retienen las representaciones de los distritos del Congreso de Carolina del Norte, izquierda y Maryland, derecha. Foto de AP / Carolyn Kaster

"¿Estamos en el tercer distrito del Congreso de Maryland?", Preguntó Karen en una visita reciente al campus de la UMBC. A pesar de hacer zoom en el mapa del distrito en Wikipedia, ninguno de los dos podía decirlo. Con buena razón - "la mantis religiosa", Como se ha llamado al tercero, tiene uno de los límites más aberrantes del país. (La universidad se encuentra justo afuera, como encontramos más tarde).

El tercer distrito del Congreso de Maryland. Wikimedia

Bienvenido a Maryland, controlado por los demócratas. El estado, junto con el control republicano de Carolina del Norte, defendió su distrito distrital contra el cargo de piratería ilegal partidista en las audiencias en la Corte Suprema de los Estados Unidos en marzo 26.

Uno podría pensar que un mapa que confunde a dos matemáticos debe estar en clara violación de la ley. De hecho, los científicos políticos y matemáticos han trabajado juntos para proponer varias criterios geometricos para dibujar distritos electorales de formas contiguas lógicas, que ahora se utilizan en varios estados de EE. UU.

Pero aquí está el problema: Gerrymandering en sí mismo no es inconstitucional. Para que la Corte Suprema se pronuncie en contra de un mapa en particular, los demandantes deben establecer que el mapa infringe algún derecho constitucional, como su derecho a igual protección o libertad de expresión. Esto crea un problema. Los criterios geométricos no detectan el partidismo. Otros criterios tradicionales, como asegurarse de que cada distrito tenga la misma población, también pueden satisfacerse fácilmente en un mapa de estado que de otra manera sería injustamente diseñado.

Entonces, ¿cómo definir un estándar para identificar un gerrymandering partidario que sea lo suficientemente grave como para ser ilegal? Los científicos matemáticos ya han encontrado soluciones prometedoras, pero nos preocupa que la Corte Suprema no tome su consejo cuando emita su decisión en junio.

Buscando respuestas

La Corte Suprema ha lidiado con la cuestión de estándares manejables al menos desde 1986, el tiempo suficiente para que el juez Antonin Scalia declarar en un fallo 2004 que como no había surgido uno todavía, el problema del gerrymandering partidista no era legalmente decidible, y por lo tanto, no deberían considerarse otras apelaciones.

Fue solo la concurrencia separada del juez Anthony Kennedy lo que mantuvo la puerta abierta. Advirtió contra el abandono de la búsqueda de un estándar demasiado pronto, diciendo que "la tecnología es tanto una amenaza como una promesa". En otras palabras, los avances tecnológicos probablemente exacerbarán el problema de la manipulación de datos, pero también podrían proporcionar una solución.

El problema ha empeorado, tal como lo predijo Kennedy. Los programas de computadora ahora pueden generar una profusión de mapas redistribuidos, todos los cuales satisfacen las limitaciones tradicionales, como la contigüidad y la población igual en todos los distritos. Entonces, el partido mayoritario puede simplemente elegir el mapa más favorable para él.

Esto fue demostrado en Elecciones 2018 de Wisconsin. Los mapas de Gerrymandered reforzados por computadora supersize el borde de 13 de los Republicanos a una mayoría de 25-asiento, aunque Los demócratas ganaron 53 por ciento del total de votos a nivel estatal.

Esperamos que los nuevos distritos parlamentarios seleccionados en todo el país después del censo de 2020 estén sujetos a un feroz gestionamiento informático aún más feroz.

Matemáticas para el rescate

Pero la segunda parte de la predicción de Kennedy también se ha hecho realidad. Las mismas herramientas que producen mapas drásticamente gerrymandered se pueden utilizar para dibujar mapas justos.

El primer paso es generar, sin intención partidista, una gran cantidad de mapas que se adhieran a los criterios tradicionales de redistribución de distritos. Esto crea una base de datos contra la cual se puede comparar cualquier mapa propuesto, mediante el uso de una fórmula matemática adecuada que mida el partidismo. A través de este proceso, los mapas con sesgo extremo aparecerán como valores atípicos claros, al igual que los puntos de datos cerca de los extremos externos de una curva de campana.

La “Brecha de eficiencia” Es una de esas fórmulas matemáticas. Mide qué tan eficientemente se usan los votos de un partido y cuánto se desperdician los votos del otro partido. Por ejemplo, un mapa puede agrupar a los votantes para minimizar su influencia en otros distritos, o distribuirlos para que no formen un bloque efectivo.

{youtube}bGLRJ12uqmk{/youtube}

También existen fórmulas alternativas. De hecho, recomendamos usar una colección de fórmulas, en lugar de solo una, para compensar las limitaciones de cada una.

Conferencias recientes En la redistribución de distritos, las comunidades de matemáticas y estadísticas se unieron en torno a este "enfoque atípico".

Superando el escepticismo

Sin embargo, lograr que la Corte Suprema acepte este enfoque requerirá superar el escepticismo que algunos jueces conservadores han expresado hacia el uso de las matemáticas y las estadísticas para establecer estándares legales.

durante Argumentos orales de octubre 2017 por un desafío a los mapas de Wisconsin, por ejemplo, el presidente del Tribunal, John Roberts, caracterizó la brecha de eficiencia como "sociable idiota", mientras que el juez Neil Gorsuch dijo que la idea de usar múltiples fórmulas para medir el gerrymandering era como agregar "una pizca de esto, una pellizco de eso "a su carne frote. Roberts también expresó su preocupación por el hecho de que el país descartaría las fórmulas estadísticas como "un montón de tonterías" y sospecharía que el tribunal del favoritismo político las adoptara.

En el Marzo audiencias 26 para el desafío de Carolina del Norte, los jueces conservadores fueron más medidos y matemáticamente inteligentes al expresar sus reservas. Esta vez, el "enfoque atípico" tomó el centro del escenario. Afirmado en la decisión del tribunal inferior y explicado en una amicus brief, también fue respaldado en argumentos orales por los jueces Elena Kagan y Sonia Sotomayor. Las dudas clave provinieron de los jueces Samuel Alito, Gorsuch y Brett Kavanaugh, quienes cuestionaron la posibilidad de definir un "valor atípico" en la práctica, en particular, estableciendo un rango de parámetros numéricos que demarcaran los mapas permisibles de los no permisibles.

La respuesta a tales objeciones, tratada con habilidad en un amicus brief de Eric Lander del MIT, es doble. En primer lugar, los mapas que se cuestionan son tan sesgados que son extremos atípicos. Se mostrarían como anomalías en cualquier prueba de partidismo. Por lo tanto, no es necesario que la Corte Suprema establezca un nivel de corte numérico en esta etapa, aunque un umbral puede, de hecho, evolucionar en el futuro. En segundo lugar, un enfoque tan atípico extremo ya es una herramienta indispensable en varias áreas de importancia nacional. Por ejemplo, se utiliza para prueba de seguridad nuclear, predecir huracanes y Evaluar la salud de las instituciones financieras..

<p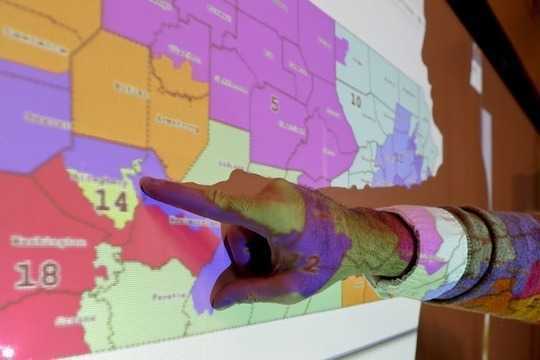 Gerrymandering partidista también ha sido un tema candente en Pennsylvania. Foto AP / Keith Srakocic

Además, este enfoque ya se ha demostrado que funciona sin problemas en casos de manipulación de datos también, como en uno de Pennsylvania. Moon Duchin, un profesor de matemáticas de la Universidad de Tufts, lo usó para analizar, en un informe solicitado por el gobernador Tom Wolf, los nuevos mapas propuestos para la justicia. Un mapa dibujado por la legislatura estatal del Partido Republicano destacó claramente como un valor extremo entre más de mil millones de mapas generados, tanto cuando se evaluó usando la brecha de eficiencia como bajo otra medida de partidismo llamada la puntuación media-mediana. Residencia en El informe de duchin, el gobernador rechazó el mapa propuesto por el Partido Republicano.

Esperamos que, impulsados ​​por grupos de ciudadanos, un número creciente de estados incorporará las matemáticas en los procedimientos de redistribución de distritos. El año pasado, por ejemplo, aprobó Missouri Enmienda 1prescribir reglas matemáticas detalladas que debe seguirse para garantizar la equidad de los distritos rediseñados. Aunque las reglas se basan en gran medida en la brecha de eficiencia, y los legisladores pueden intentar anularlos por completo - El hecho de que los ciudadanos comunes y corrientes. votó abrumadoramente (62 por ciento a 38 por ciento) a favor de una medida que incorpore matemáticas de este tipo es realmente un establecimiento de precedentes.

Tales desarrollos se notaron en los argumentos orales de marzo de 26, cuando algunos jueces se preguntaron si, a la luz de las iniciativas estatales, la Corte Suprema realmente tenía que intervenir. Como los abogados de los ciudadanos señalaron, sin embargo, hay muy pocos estados al este del Mississippi donde se permiten tales iniciativas ciudadanas. (Carolina del Norte no es uno de ellos). Le corresponde a la corte tomar la iniciativa a nivel nacional.

Mejorado por el poder de las computadoras, el gerrymandering partidista representa una creciente amenaza para el modo de democracia estadounidense. Las normas viables basadas en principios matemáticos sólidos pueden ser las únicas herramientas para contrarrestar esta amenaza. Instamos a la Corte Suprema a ser receptiva a tales estándares, permitiendo así a los ciudadanos proteger su derecho a una representación justa.

Sobre el Autor

Manil Suri, catedrático de Matemáticas y Estadística, Universidad de Maryland, Condado de Baltimore y Karen Saxe, profesora de Matemáticas, Emerita, Macalester College

Este artículo se republica de La conversación bajo una licencia Creative Commons. Leer el articulo original.

Libros relacionados

at InnerSelf Market y Amazon